本文大部分来源于胡渊鸣学长的2013年国家集训队论文《浅谈信息学竞赛中概率论的基础与应用》
从理论的角度?来学习概率......但由于本人实力比较弱,欢迎指正
部分公式的表达可能不太严谨......能理解就行
欢迎转载,只是需要注明出处....
1.概率
我们定义这么一个函数,
函数$P(A)$,表示 事件$A$ 发生的可能性的大小,称作概率测度
此时,$A$是事件集合$F$的一个子集,注意事件本身也有可能是一个集合
并且所有的事件$A$都可以看做是样本空间$\Omega$的一个子集
那么,合法的三元组$(\Omega, F, P)$为就可以被称为概率空间
这里,合法的定义为:
$$\forall x \in \Omega, P(x) \geq 0$$
$$P(\Omega) = 1$$
$$A \cap B = \varnothing \to P(A \cup B) = P(A) + P(B)$$
$\Omega$是全集
$F$是囊括了所有的事件
$P$是一种把集合映射到实数上的函数,其意义为事件发生的可能性大小
$P$比较好理解
那$F$和$\Omega$的区别在哪里呢?
比如抛硬币
全集$\Omega$为{ 正面向上,反面向上,立起 };
记正面向上为$A$, 反面向上为$B$,立起为$C$
那么$F$应为$\{ \{A, B, C\}, \{A, B\}, \{A, C\}, \{B, C\}, \{A\}, \{B\}, \{C\}, \varnothing \}$
也就是说,全集类似于所有最小单位的集合,而$F$是全集中的元素组合出的集合
2.条件概率
在我们知道了一些黑暗的事情后,事件的概率是会改变的
比如在街上随便找个人,他是男生的概率近似于$0.5$
但是,如果你知道他学$OI$,那么他是男生的概率可以提升至$0.999999$
条件概率的公式为
$$P(A | B) = \frac{P(A \cap B)}{P(B)}$$
实际上,条件概率是变换样本空间的一种思考方式
比如上面的例子,随便找个人,那么样本空间是全球的人
但是如果他学$OI$,那么我们考虑的人就只是学$OI$中的人
可以认为,条件概率表示了两个样本空间之间概率测度的关系
也就是用一个实数来表示 (你是个普通人,你要$ak$) 和(你是神仙,你要$ak$)这种现实差的可能性...
大概?
3.全概率公式
如果$B_1, B_2 ...... B_n$是样本空间的一个划分,那么有
$$P(A) = \sum\limits_{i} P(A | B_i) * P(B_i)$$
好比,你要$ak$的概率可以拆分成
(你是女生,你要$ak$),(你是男生,你要$ak$),
(你是人妖,你要$ak$),(你无性别,你要$ak$),
四部分的概率,而通过条件概率,我们就能通过每部分的概率得出总概率
注意划分的意义:
$\forall B_i, B_j \in \Omega,B_i \cap B_j = \varnothing$
$\bigcup B_i = \Omega$
4.贝叶斯公式
$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$
转化成$P(A \cap B)$就能证明了...
可以有效的计算逆向概率
其实体现了两个不同样本空间对同一样本空间的关系的关系(有点绕)...
其中,$P(A), P(B)$可以用全概率公式展开
但是太鬼畜了,公式难打,就不展开了
5.随机变量
随机变量一点都不有趣,它既不随机,也不是一个变量
随机变量是定义在$\Omega$上的一个函数
也就是函数$f : \Omega \to R$是一个随机变量
通过随机变量,我们可以通过考虑值来考虑事件
可以认为这是对$\Omega$的一种划分,把$f(X)$相同的$X$划分到了一起的一种方法.....
对于一个$\Omega$,随机变量有很多个
但是,我们一般都默认是权值......也有认为是次数的时候......
6.期望
定义随机变量$X$的期望为
$$E[X] = \sum\limits_{x} P(x) X(x) = \sum\limits_{x} xP(X = x)$$
其中,$P(X= x)$表示$\sum\limits_{y} P(y)[X(y) = x]$
期望可以理解为加权平均
这里本人有一个奇怪的疑惑?
在做期望$dp$的时候,转移中根本没有体现随机变量这种函数样的东西....
所以期望到底代表了什么?
于是从百度百科拿了个例子
城市中有$0, 1, 2, 3$个孩子的家庭的概率分别为$0.01,0.9,0.06,0.03$
那么我们定义随机变量$X$表示城市中一个家庭中孩子的数量
(这里的$X$大概是这个意思:比如$X(a) = 1$表示$a$号家庭中有1个孩子,$X(b) = 2$表示$b$号家庭中有2个儿子)
那么,根据公式有$E[X] = 1.11$,表示城市中一个家庭孩子的平均数量
也就是说,期望体现了所有取值下函数(随机变量)$X$的一个平均值
(跟积分很像是不是...)
我们考虑这么一类随机变量$X[S](x)$,表示某个集合中$x$元素达到满足$S$条件的代价
那么,$E[X[S]]$就表示某个集合达到满足$S$条件的平均代价
同样的,我们还可以考虑构造$E[X[S][T]]$表示某个集合从满足$S$条件达到满足$T$条件的平均代价
$S$条件甚至可以是限制为某个集合的子集这种.......神奇......
可以发现,实际上它才是我们平时$dp$的真面目......
根据期望的公式,我们有两个计算方式:
1.考虑枚举每一个事物,计算其概率再求期望
2.考虑枚举权值$x$,计算权值的概率求期望
7.独立事件
如果两个事件$A, B$,满足$P(A \cap B) = P(A) * P(B)$
那么,我们就称$A, B$为独立事件
当然,有时我们可以通过人脑智慧判断$A, B$独不独立($A$不影响$B$,$B$不影响$A$)后,
使用$P(A \cap B) = P(A) * P(B)$这条定义......(定义当性质用真的好吗?)
8.期望的相关运算
如果你英文和数学足够好
请参见
有些证明参照上面的链接
特殊的期望
$$\forall x \in \Omega, X(x) = c \to E[X] = c$$
期望的线性性质
$$E[aX + bY] = aE[X] + bE[Y]$$
期望的积
两个随机变量$X, Y$
满足$\forall x_1 \in D_X,y_1 \in D_Y,P(X = x_1 \cap Y = y_1) = P(X = x_1) P(Y = y_1)$
则称它们为独立的随机变量
那么,它们满足
$$E[XY] = E[X]E[Y]$$
全期望公式
$$E[E[X | Y]] = E[X]$$
拒绝纸上谈兵......
上菜............
一些可食用的题目
首先我们来板刷洛谷吧...
luoguP1850 换教室

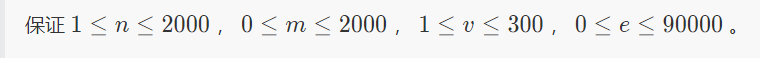
令$dp[i][j][0/1]$表示到了第$i$天,换了$j$次教师,第$i -1$天在原来的教室还是换了的最小期望
注意转移的时候考虑完整,不要漏情况了
代码是以前的,风格自己也无法掌控...


#include#define INF 1047483647#define ri register int#define dl doubleusing namespace std;inline dl min(dl a, dl b) { return (a < b) ? a : b;}inline int imin(int a, int b) { int c = (a - b) >> 31; return a & c | b & ~c;}int n, m, v, e;int c[2005], d[2005];int dis[305][305];dl dp[2005][2005][2];dl k[2005], dk[2005];dl ans = INF;inline void Init() { for(ri i = 1; i <= v; i ++) for(ri j = i + 1; j <= v; j ++) dis[i][j] = dis[j][i] = INF; for(ri i = 1; i <= n; i ++) for(ri j = 0; j <= m; j ++) dp[i][j][0] = dp[i][j][1] = INF; dp[1][0][0] = dp[1][1][1] = 0;}inline void In() { int u, vv, w; scanf("%d%d", &n, &m); scanf("%d%d", &v, &e); for(ri i = 1; i <= n; i ++) scanf("%d", &c[i]); for(ri j = 1; j <= n; j ++) scanf("%d", &d[j]); for(ri i = 1; i <= n; i ++) scanf("%lf", &k[i]), dk[i] = 1.0 - k[i]; Init(); for(ri i = 1; i <= e; i ++) { scanf("%d%d%d", &u, &vv, &w); dis[u][vv] = dis[vv][u] = imin(w, dis[u][vv]); }}inline void Floyd() { for(ri l = 1; l <= v; l ++) for(ri i = 1; i <= v; i ++) for(ri j = 1; j <= v; j ++) dis[i][j] = imin(dis[i][j], dis[i][l] + dis[l][j]);}inline void DP() { for(ri i = 2; i <= n; i ++) { dp[i][0][0] = dp[i - 1][0][0] + dis[c[i - 1]][c[i]]; int tmp1 = dis[c[i - 1]][c[i]]; int tmp2 = dis[d[i - 1]][c[i]]; int tmp3 = dis[d[i - 1]][d[i]]; int tmp4 = dis[c[i - 1]][d[i]]; for(ri j = 1; j <= m; j ++) { dp[i][j][0] = min(dp[i - 1][j][0] + tmp1, dp[i - 1][j][1] + tmp1 * dk[i - 1] + tmp2 * k[i - 1]); //嗯。。。。。。 dp[i][j][1] = min(dp[i - 1][j - 1][0] + tmp1 * dk[i] + tmp4 * k[i], dp[i - 1][j - 1][1] + tmp1 * dk[i - 1] * dk[i] + tmp2 * k[i - 1] * dk[i] + tmp4 * dk[i - 1] * k[i] + tmp3 * k[i - 1] * k[i]); } }}inline void Get_ans() { for(ri i = 1; i <= m; i ++) ans = min(ans, min(dp[n][i][0], dp[n][i][1])); ans = min(ans, dp[n][0][0]); printf("%.2lf", ans);}inline void Work() { Floyd(); DP(); Get_ans();}int main() { In(); Work(); return 0;}
luoguP3802 小魔女帕琪

小魔女帕琪到底是谁啊?蕾咪那么可爱,为什么要打啊....
然后....不懂题解在写什么东西....
这题其实还是有点意思的
首先考虑通过枚举来求期望
发现权值都是统一的1,所以考虑求出概率和就行了
可以发现,挥霍完所有的能量晶体对应一个长度为$S = \sum\limits_{i = 1}^7 a[i]$的排列
那么,我们需要枚举这个连续$7$个元素出现的位置,自然有$S - 6$个不同的位置
接着,我们选中这$7$个元素,有$\prod\limits_{i = 1}^7 a[i]$种选法
这$7$个元素在指定的位置任意排列,剩余的$S - 7$个元素也任意排列
并且总方案数为$S!$,且概率相同,那么最终概率和为$$\frac{(S - 6) * (S - 7)! * 7! * \prod\limits_{i =1}^7 a[i]}{S!}$$
注:输出$0.000$是什么鬼,大部分人的程序好像都是错的,$0\;0\;1\;1\;0\;0\;0$就不行了......唉.....


#include#include using namespace std;#define de long doublede ans = 5040;de a[20], S;int main() { for(int i = 1; i <= 7; i ++) { cin >> a[i]; S += a[i]; if(a[i] == 0) { printf("0.000\n"); return 0; } } for(int i = 1; i <= 7; i ++) ans = ans * a[i] / (S - i + 1); printf("%.3Lf\n", ans * (S - 6)); return 0;}
luoguP4316 绿豆蛙的归宿


两种方法
第一种是利用期望的线性性质,总长度期望 = 所有的边的期望和,那么弄出每一条边的概率即可


#include#include using namespace std;extern inline char gc() { static char RR[23456], *S = RR + 23333, *T = RR + 23333; if(S == T) fread(RR, 1, 23333, stdin), S = RR; return *S ++;}inline int read() { int p = 0, w = 1; char c = gc(); while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); } while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc(); return p * w;}#define de double#define ri register int#define sid 200050de f[sid], ans;int n, m, cnp, du[sid], in[sid], cd[sid], q[sid];int cap[sid], nxt[sid], node[sid], fee[sid];inline void addeg(int u, int v, int w) { nxt[++ cnp] = cap[u]; cap[u] = cnp; node[cnp] = v; fee[cnp] = w;}int main() { n = read(); m = read(); for(ri i = 1; i <= m; i ++) { int u = read(), v = read(), w = read(); addeg(u, v, w); du[v] ++; in[v] ++; cd[u] ++; } int fr = 1, to = 0; q[++ to] = 1; f[1] = 1; while(fr <= to) { int o = q[fr ++]; for(ri i = cap[o]; i; i = nxt[i]) { int d = node[i]; f[d] += f[o] / (de)(cd[o]); ans += fee[i] * f[o] / (de)(cd[o]); in[d] --; if(!in[d]) q[++ to] = d; } } printf("%.2lf\n", ans); return 0;}
第二种方法是直接在拓扑上$dp$
由于是期望$dp$,那么需要逆推......
至于为什么?因为从点$x$必须要走到$n$,但是从点$1$不一定会走到$x$
并且还可以排除很多合法的情况
何乐而不为?代码就......咕咕咕咕咕咕咕咕
luoguP1297 [国家集训队]单选错位


挺简单的......
由于权值是$1$,因此实际上只要求概率和
对于第$i$道题,做对它的要求为第$i$题和第$i - 1$题的答案一样
因此,其概率为$\frac{min(a[i], a[i - 1])}{a[i] * a[i - 1]} = \frac{1}{max(a[i], a[i - 1])}$


#include#include using namespace std;#define de double#define ri register int#define mod 100000001de ans;int n, A, B, C;int a, a1, b, c, d;int main() { cin >> n >> A >> B >> C >> a; a1 = a % C + 1; d = a % C + 1; for(ri i = 2; i <= n; i ++) { c = (1ll * a * A % mod + B) % mod; b = c % C + 1; ans += 1.0 / (de)(max(d, b)); a = c; d = b; } ans += 1.0 / (de)(max(b, a1)); printf("%.3lf\n", ans); return 0;}
luoguP1365 WJMZBMR打osu! / Easy

略有感触......
设一段区间的长度为$n$,那么它对答案的贡献为$n^2$,这不是一个线性的变换,我们想个办法让它变为线性的
只要变换是线性的,那么我们可以直接使用期望$dp$
考虑增量,$(n + 1)^2 - n^2 = 2 * n + 1$,发现增量是线性的
那么我们直接统计增量的影响,而不是直接统计区间的影响
令$f[i]$表示$dp$到了第$i$位的期望得分,$g[i]$表示$dp$到了$i$位的前置期望$o$长度
那么有
$$f[i] = f[i - 1] + g[i - 1] * 2 + 1, g[i] = g[i - 1] + 1 \;(s[i] == o)......(1)$$
$$f[i] = f[i - 1], g[i] = 0\;(s[i] == x)......(2)$$
$$f[i] = \frac{(1) + (2)}{2}, g[i] = \frac{(1) + (2)}{2}\;(s[i] == ?)$$


#include#include #include using namespace std;#define de double#define ri register int#define sid 2000050int n;char s[sid];de f[sid], g[sid];int main() { cin >> n; scanf("%s", s + 1); for(ri i = 1; i <= n; i ++) { if(s[i] != 'x') { f[i] += f[i - 1] + g[i - 1] * 2 + 1; g[i] += g[i - 1] + 1; } if(s[i] != 'o') f[i] += f[i - 1]; if(s[i] == '?') f[i] /= 2.0, g[i] /= 2.0; } printf("%.4lf\n", f[n]); return 0;}
luoguP3924 康娜的线段树

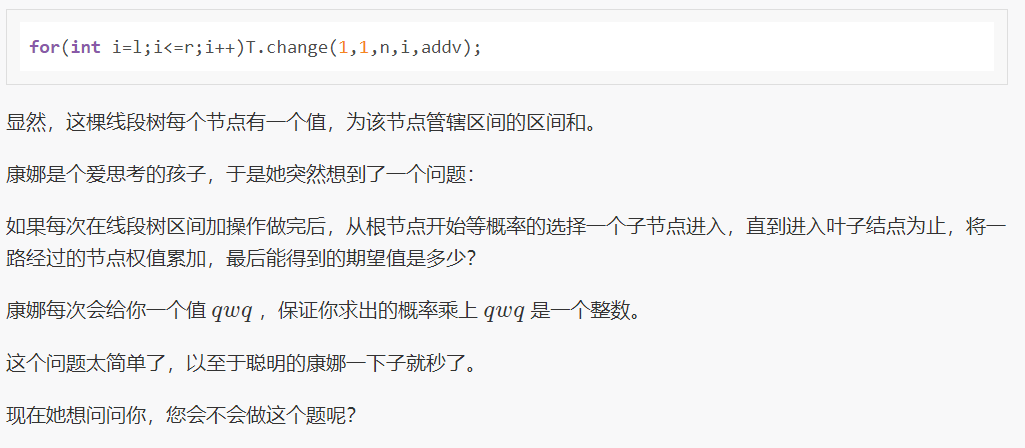

既然题目名字叫线段树,那我们就用线段树来做.......好像只有我一个用线段树卡过去了?
运用期望的线性性质,总期望可以拆分成线段树中的每个节点的期望的和。
对于线段树中的每个节点,我们维护这么几个信息
$v:$,线段树的这个节点及其子树内的概率的权值和(具体看代码吧,不方便用言语描述)
$p:$,线段树的这个节点的概率
每次修改的时候,完整包含的区间直接调用$v$,否则计算出查询区间与当前区间的交集$* p$的值
具体看代码吧
复杂度$O(n \log n)$
注:$ans$要用$long\;double$存精度才够...
注2:输入和输出优化不加你就$TTT$,虽然我没有$T$过


#include#include #include using namespace std;extern inline char gc() { static char RR[23456], *S = RR + 23333, *T = RR + 23333; if(S == T) fread(RR, 1, 23333, stdin), S = RR; return *S ++;}inline int read() { int p = 0, w = 1; char c = gc(); while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); } while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc(); return p * w;}int wr[50], rw;#define pc(z) *I ++ = zchar WR[20000005], *I = WR;template inline void write(re x) { if(!x) pc('0'); if(x < 0) x = -x, pc('-'); while(x) wr[++ rw] = x % 10, x /= 10; while(rw) pc(wr[rw --] + '0'); pc('\n');}#define sid 1005000#define ri register int#define ll long long#define de long doubleint n, m, mmp;int a[sid], s[sid * 4];ll k[sid * 4], v[sid * 4];de ans;#define ls (o << 1)#define rs (o << 1 | 1)void build(int o, int l, int r, int p) { k[o] = p; if(l == r) { a[l] = read(); ans += (de)k[o] * a[l]; v[o] = p; s[o] = a[l]; return; } int mid = (l + r) >> 1; build(ls, l, mid, p / 2); build(rs, mid + 1, r, p / 2); s[o] = s[ls] + s[rs]; ans += (de)k[o] * s[o]; v[o] = v[ls] + v[rs] + k[o] * (r - l + 1);}ll query(int o, int l, int r, int ml, int mr) { if(ml > r || mr < l) return 0; if(ml <= l && mr >= r) return v[o]; int mid = (l + r) >> 1; ll tmp = 0; if(ml >= l && mr <= r) tmp = k[o] * (mr - ml + 1); if(ml < l) tmp = k[o] * (mr - l + 1); if(mr > r) tmp = k[o] * (r - ml + 1); return query(ls, l, mid, ml, mr) + query(rs, mid + 1, r, ml, mr) + tmp;}int main() { n = read(); m = read(); mmp = read(); int p = 1 << 22; build(1, 1, n, p); for(ri i = 1; i <= m; i ++) { int l = read(), r = read(), x = read(); ans += (de)query(1, 1, n, l, r) * x; write((ll)((de)(ans / p) * mmp)); } fwrite(WR, 1, I - WR, stdout); return 0;}
luoguP2473 [SCOI2008]奖励关

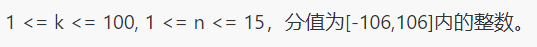
首先,我们注意到这涉及到最优策略的问题,由于这题不可贪心,因此我们需要把所有的决策所需的条件枚举出来
也就是说,我们需要状态压缩来确定如何做决策,又由于期望逆推
设$f[i][S]$表示第$i$轮状态为$S$,第$i + 1$至$k$轮的最大期望得分
枚举宝物$j$
如果$j$能选,那么$f[i][S] += \frac{max(f[i + 1][S], val[j] + f[i + 1][S | 2^j])}{n}$
否则,$f[i][S] += \frac{f[i + 1][S]}{n}$
$f[1][0]$即为所求
事实上,逆推用$dfs$实现更为的合适...


#include#include using namespace std;#define sid 105#define de double#define ri register intint n, k;int bit[50];de f[sid][130050];int val[sid], pre[sid];int main() { cin >> k >> n; for(ri i = 0; i <= 20; i ++) bit[i] = 1 << i; for(ri i = 1; i <= n; i ++) { cin >> val[i]; int w; while(1) { cin >> w; if(w == 0) break; pre[i] |= bit[w - 1]; } } for(ri i = k; i; i --) for(ri j = 0; j <= bit[n] - 1; j ++) { for(ri o = 1; o <= n; o ++) if((j & pre[o]) == pre[o]) f[i][j] += max(f[i + 1][j], val[o] + f[i + 1][j | bit[o - 1]]); else f[i][j] += f[i + 1][j]; f[i][j] /= (de)n; } printf("%.6lf\n", f[1][0]); return 0;}
luoguP3412 仓鼠找sugar II


仓鼠找sugar I是啥来着?忘了...
首先求总期望的话,用期望的线性性质拆分成每条边的期望
对于一条边$u - v$而言,$u \to v$和$v \to u$的期望是不同的
考虑分开统计,记$u \to v$的期望步数为$f[u \to v]$
那么有$f[u \to fa] = \frac{1}{du[u]} + \sum\limits_{v \in son_u} \frac{f[u \to fa] + f[v \to u] + 1}{du[u]}$
化简后为$f[u \to fa] = du[u] + \sum\limits_{v \in son_u} f[v \to u]$
对于一个点而言,通过递推式,我们发现,除了它走向父亲的边期望走过1次以外,其余边恰好期望走过2次!
因此有$f[u \to fa] = 2 * sz[u] - 1$
同时对于边$u \to v$,有$\frac{sz[u] *(n - sz[u])}{n^2}$的概率经过它,对于边$v \to u$同理
$O(n)$统计即可
至于有理数取模,把$n^2$提出来最后乘逆元就行


#includeusing namespace std;extern inline char gc() { static char RR[23456], *S = RR + 23333, *T = RR + 23333; if(S == T) fread(RR, 1, 23333, stdin), S = RR; return *S ++;}inline int read() { int p = 0, w = 1; char c = gc(); while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); } while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc(); return p * w;}#define mod 998244353#define ll long long#define ri register int#define sid 200050int n, cnp, ans;int nxt[sid], node[sid], cap[sid], sz[sid];inline void adeg(int u, int v) { nxt[++ cnp] = cap[u]; cap[u] = cnp; node[cnp] = v;}inline int fp(int a, int k) { int ret = 1; for( ; k; k >>= 1, a = 1ll * a * a % mod) if(k & 1) ret = 1ll * ret * a % mod; return ret;}#define cur node[i]void dfs(int o, int fa) { sz[o] = 1; for(int i = cap[o]; i; i = nxt[i]) if(cur != fa) dfs(cur, o), sz[o] += sz[cur]; ans = (ans + 1ll * sz[o] * (n - sz[o]) % mod * (n * 2 - 2) % mod) % mod;}int main() { n = read(); for(ri i = 1; i < n; i ++) { int u = read(), v = read(); adeg(u, v); adeg(v, u); } dfs(1, 0); printf("%d\n", 1ll * ans * fp(1ll * n * n % mod, mod - 2) % mod); return 0;}
luoguP2221 [HAOI2012]高速公路

$n \leqslant 10^5$
首先,使用期望的线性性质,整个区间的期望 = 每个节点的期望之和
那么,如果记$E[x]$为$x$点出现的期望
那么有$E[x] = v[x] * (x - l + 1) * (r - x + 1)$
现在要区间询问,于是考虑求和$E[l, r] = \sum\limits_{i = l}^r E[i] = \sum\limits_{i = l}^r v[i] * (i - l + 1) * (r - i + 1)$
在线段树中维护$v[i]*i^2, v[i]*i, v[i]$即可回答
代码是以前写的......画风自适应吧.....复杂度$O(n \log n)$


#include#define ri register int#define ll long long#define int long long#define sid 2000500using namespace std;#define getchar() *S ++char RR[30000005], *S = RR;inline int read() { int p = 0, w = 1; char c = getchar(); while(c > '9' || c < '0') { if(c == '-') w = -1; c = getchar(); } while(c >= '0' && c <= '9') { p = p * 10 + c - '0'; c = getchar(); } return p * w;}inline int Get_Opt() { char c = getchar(); while(c > 'Z' || c < 'A') c = getchar(); if(c == 'C') return 1; else return 2;}int n, m, ml, mr;ll s1, s2, s3, mc;ll p1[sid], p2[sid];ll sum1[sid], sum2[sid], sum3[sid], lz[sid];inline ll gcd(ll a, ll b) { return (b) ? gcd(b, a % b) : a;}inline void Update(int p) { sum1[p] = sum1[p << 1] + sum1[p << 1 | 1]; sum2[p] = sum2[p << 1] + sum2[p << 1 | 1]; sum3[p] = sum3[p << 1] + sum3[p << 1 | 1];}inline void Pushdown(int p, int l, int r) { if(!lz[p]) return; int ls = (p << 1), rs = (p << 1 | 1); int mid = (l + r) >> 1; lz[ls] += lz[p]; lz[rs] += lz[p]; sum1[ls] += (mid - l + 1) * lz[p]; sum1[rs] += (r - mid) * lz[p]; sum2[ls] += (p1[mid] - p1[l - 1]) * lz[p]; sum2[rs] += (p1[r] - p1[mid]) * lz[p]; sum3[ls] += (p2[mid] - p2[l - 1]) * lz[p]; sum3[rs] += (p2[r] - p2[mid]) * lz[p]; lz[p] = 0;}inline void Modify(int p, int l, int r) { if(ml <= l && mr >= r) { sum1[p] += (r - l + 1) * mc; sum2[p] += (p1[r] - p1[l - 1]) * mc; sum3[p] += (p2[r] - p2[l - 1]) * mc; lz[p] += mc; return; } Pushdown(p, l, r); int mid = (l + r) >> 1; if(ml <= mid) Modify(p << 1, l, mid); if(mr > mid) Modify(p << 1 | 1, mid + 1, r); Update(p);}inline void Query(int p, int l, int r) { if(ml <= l && mr >= r) { s1 += sum1[p]; s2 += sum2[p]; s3 += sum3[p]; return; } Pushdown(p, l, r); int mid = (l + r) >> 1; if(ml <= mid) Query(p << 1, l, mid); if(mr > mid) Query(p << 1 | 1, mid + 1, r); Update(p);}inline void Init() { for(ri i = 1; i <= n - 1; i ++) { p1[i] = i + p1[i - 1]; p2[i] = i * i + p2[i - 1]; }}signed main() { fread(RR, 1, sizeof(RR), stdin); n = read(); m = read(); Init(); for(ri i = 1; i <= m; i ++) { int opt = Get_Opt(), x = read(), y = read() - 1; if(x > y) { printf("0/0\n"); continue; } if(opt == 2) { ml = x; mr = y; s1 = s2 = s3 = 0; Query(1, 1, n); ll ans1 = (y - x + 1) * (y - x + 2) / 2; ll ans2 = -s3 + (x + y) * s2 + (y - x - y * x + 1) * s1; ll d = gcd(ans1, ans2); printf("%lld/%lld\n", ans2 / d, ans1 / d); } else { ml = x; mr = y; mc = read(); Modify(1, 1, n); } } return 0;}
luoguP3211 [HNOI2011]XOR和路径


比较经典的高斯消元模型,求期望使用逆推
由于是异或和,因此按位考虑
$f[i][0 / 1]$表示$i$号节点走到$n$号节点的路径$xor$和在第$i$位为$0 / 1$时的期望
注意到$f[i][0] + f[i][1] = 1$
因此$f[i][1] = \frac{1}{du[i]} * \sum\limits_{(i, v) = 1} f[v][0] + \sum\limits_{(i, v) = 0} f[v][1]$
$f[i][1] = \frac{1}{du[i]} * \sum\limits_{(i, v) = 1} (1 - f[v][1]) + \sum\limits_{(i,v) = 0} f[v][1]$
注意到$f$值之间互相转移,因此使用高斯消元
$f[i][1] * du[i] + \sum\limits_{(i, v) = 1} f[v][1] - \sum\limits_{(i, v) = 0} f[v][1] = \sum\limits_{(i, v) = 1} 1$
注意$f[n][1] = 0$


#include#include #include using namespace std;extern inline char gc() { static char RR[23456], *S = RR + 23333, *T = RR + 23333; if(S == T) fread(RR, 1, 23333, stdin), S = RR; return *S ++;}inline int read() { int p = 0, w = 1; char c = gc(); while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); } while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc(); return p * w;}#define ri register int#define de double#define sid 205#define eid 30005int n, m, cnp, bit[50];int du[sid], cap[sid], node[eid], nxt[eid], fee[eid];inline void addedge(int u, int v, int w) { du[u] ++; nxt[++ cnp] = cap[u]; cap[u] = cnp; node[cnp] = v; fee[cnp] = w;}de ans, f[sid][sid];#define cur node[i]void Guass() { for(ri i = 1; i <= n; i ++) { int p = i; for(ri j = i; j <= n; j ++) if(fabs(f[p][i]) < fabs(f[j][i])) p = j; swap(f[i], f[p]); for(ri j = i + 1; j <= n; j ++) { de t = f[j][i] / f[i][i]; for(ri k = i; k <= n + 1; k ++) f[j][k] -= t * f[i][k]; } } for(ri i = n; i >= 1; i --) { f[i][n + 1] = f[i][n + 1] / f[i][i]; for(ri j = i - 1; j >= 1; j --) f[j][n + 1] -= f[i][n + 1] * f[j][i]; }}int main() { n = read(); m = read(); for(ri i = 1; i <= m; i ++) { int u = read(), v = read(), w = read(); if(u == v) addedge(u, v, w); else addedge(u, v, w), addedge(v, u, w); } for(ri I = 0; I <= 30; I ++) { bit[I] = 1 << I; f[n][n] = 1; for(ri j = 1; j < n; j ++) { f[j][j] = du[j]; for(ri i = cap[j]; i; i = nxt[i]) if(fee[i] & bit[I]) f[j][cur] ++, f[j][n + 1] ++; else f[j][cur] --; } Guass(); ans += bit[I] * f[1][n + 1]; for(ri i = 1; i <= n; i ++) for(ri j = 1; j <= n + 1; j ++) f[i][j] = 0; } printf("%.3lf\n", ans); return 0;}
为了更好的阅读体验,更好的骗访问量,之后的就单篇单篇的发吧
去数学 / 动态规划随便翻翻应该就有了...如果我勤快的话